2 Model-based inference

2.1 Introduction

Suppose you have been tasked with estimating the fraction of a population that supports increasing legal immigration limits. You have a sample of data on some individual respondents’ support for the policy, but you don’t know exactly how this data was sampled. How should you use the information you know (the data) to make a best guess about the information you don’t know (the fraction of the population)?

The design-based approach that we discussed in the previous chapter is a coherent and internally consistent framework for estimating quantities and quantifying uncertainty, but this crisp conceptual clarity comes from having exact knowledge of the sampling design. Going back to our immigration example, a reasonable approach is to use the fraction of the sample that supports the policy as the best guess about the fraction of the population. As we saw in the last chapter, a simple random sample would justify this approach.

But how does one perform estimation and inference when lacking complete information about the sampling design? How do we proceed with inference if outcomes are random due to nonresponse or measurement error? What if we would like to make inferences about a population not covered in the sampling frame? In these cases, inference requires additional information that can be incorporated via a statistical model. A model-based approach to statistical inference views the data $X_1,\ldots, X_n$ as a set of random variables that follow some probability distribution. The measurements in the actual sample, $x_1, \ldots, x_n$, are realizations of these random variables. The probability distribution of $X_1,\ldots, X_n$ is the model for the data and all inferences are based on it. Models can be very specific – for example, a researcher might assume the data are normally distributed – or can be very general – for example, the distribution of the data has finite mean and variance.

The focus of this chapter (and most of introductory statistics) will be on statistical models that assume units are independent and identically distributed or, more succinctly, iid. This assumption means that each unit gives us new information about the same underlying data-generating process. Because this assumption is often motivated by a probability sample from a population, some authors also refer to this as a random sampling assumption. The “sample” refers to the idea that our data is a subset of some larger population. The “random” modifier means that the subset was chosen by an uncertain process that did not favor one type of person versus another.

Why focus on iid/random samples even though many data sets are at least partially non-random or represent the entire population rather than a subset? Consider the famous story of a drunkard’s search for a two-dollar bill lost in downtown Boston:¹

“I lost a $2 bill down on Atlantic Avenue,” said the man.

“What’s that?” asked the puzzled officer. “You lost a $2 bill on Atlantic Avenue? Then why are you hunting around here in Copley Square?”

“Because,” said the man as he turned away and continued his hunt on his hands and knees, “the light’s better up here.”

Like the poor drunkard, we focus on searching an area (random samples) that are easier to search because there is more light or, more accurately, easier math. Unlike this apocryphal tale, our search will help us better understand the darkness of non-random samples because the core ideas and intuitions from random sampling form the basis for the theoretical extensions into more exotic settings.

This chapter has two goals. First, we will introduce the entire model-based framework of estimation and estimators. We will discuss different ways to compare the properties of estimators. Most of these properties will be similar to those of the design-based framework, except the properties will be with respect to the model rather than the sampling design. (The core questions of quantitative research largely remain the same, but we replace specifying the sampling design with the specification of a probabilistic model for our data.) Second, we will establish key properties for a general class of estimators that can be written as a sample mean. These results are useful in their own right since these estimators are ubiquitous, but the derivations also provide examples of how we establish such results. Building comfort with these proofs helps us understand the arguments about novel estimators that we inevitably see over the course of our careers.

2.2 Probability vs inference: the big picture

Probability is the mathematical study of uncertain events and is the basis of the mathematical study of estimation. In probability, we assume we know the truth of the world (how many blue and red balls are in the urn) and calculate the probability of possible events (getting more than five red balls when drawing ten from the urn). Estimation works in reverse. Someone hands you five balls, 2 red and 3 blue, and your task is to guess the contents of the urn from which they came. With estimation, we use our observed data to make an inference about the data-generating process.

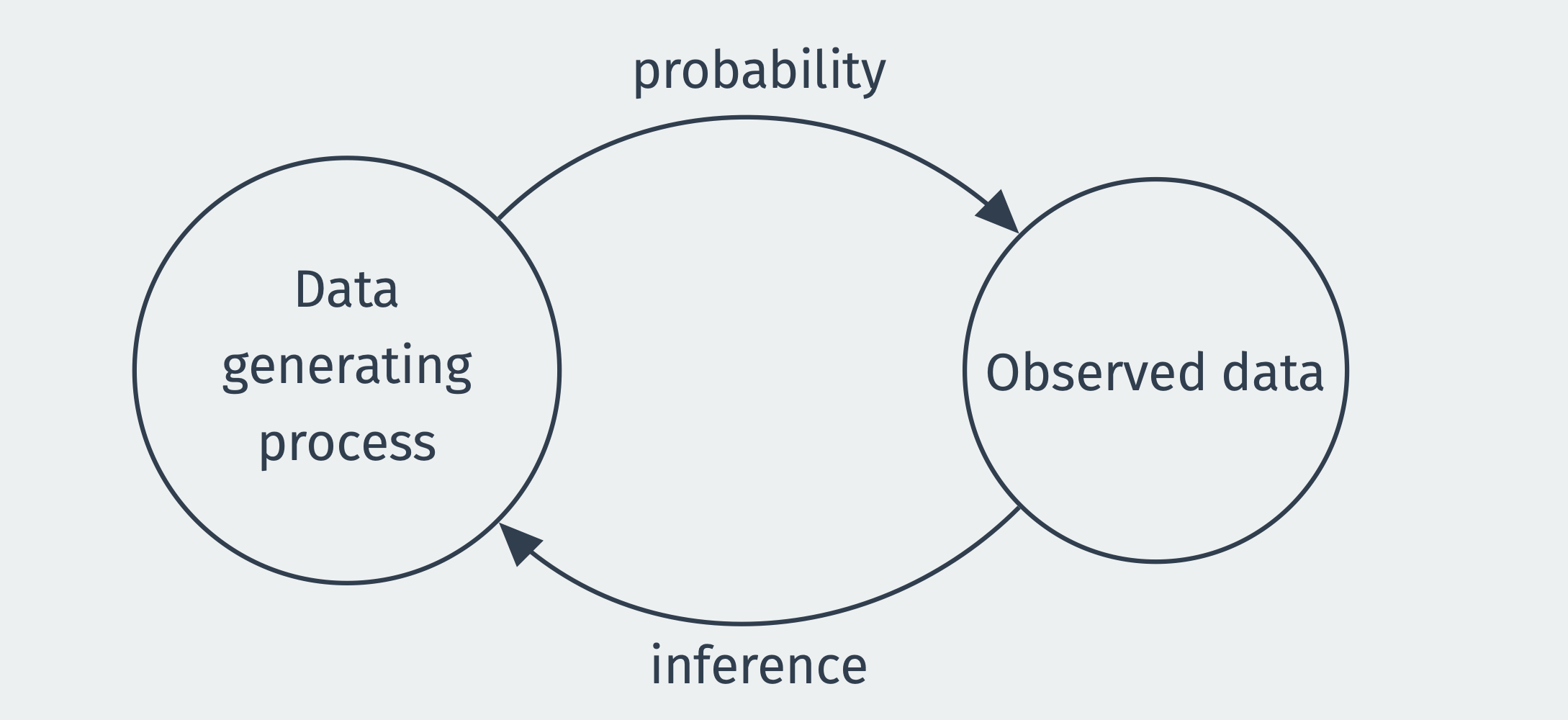
An estimator is a rule for converting our data into a best guess about some unknown quantity, such as the percent of balls in the urn, or, to use our example from the introduction, the fraction of the public supporting increasing legal immigration limits. For example, an estimator could be a rule that the proportion of red balls that you draw from the urn is a good guess for the proportion of red balls that you would find if you looked inside the urn.

We prefer to use good estimators rather than bad estimators. But what makes an estimator good or bad? In our red ball example, an estimator that always returns the value 3 is probably bad. Still, it will be helpful for us to formally define and explore properties of estimators that will allow us to compare them and choose the good over the bad. We begin with an example that highlights two estimators that at first glance may seem similar.

Example 2.1 (Randomized control trial) Suppose we are conducting a randomized experiment on framing effects. All respondents receive factual information about current immigration levels. Those in the treatment group ($D_i = 1$) receive additional information about the positive benefits of immigration, while those in the control group ($D_i = 0$) receive no additional framing. The outcome is a binary outcome, whether the respondent supports increasing legal immigration limits ($Y_i = 1$) or not ($Y_i = 0$). The observed data consists of $n$ pairs of random variables, the outcome, and the treatment assignment: $\{(Y_1, D_1), \ldots, (Y_n, D_n)\}$.

Define the two sample means/proportions in each group as \[ \Ybar_1 = \frac{1}{n_1} \sum_{i: D_i = 1} Y_i, \qquad\qquad \Ybar_0 = \frac{1}{n_0} \sum_{i: D_i = 0} Y_i, \] where $n_1 = \sum_{i=1}^n D_i$ is the number of treated units and $n_0 = n - n_1$ is the number of control units.

A standard estimator for the treatment effect in a study such as this would be the difference in means, $\Ybar_1 - \Ybar_0$. But this is only one of many possible estimators. We could also estimate the effect by taking this difference in means separately by party identification and then averaging those party-specific effects by the size of those groups. This estimator is commonly called a poststratification estimator. Which of these two estimators we should prefer is at first glance unclear.

We now turn to the same key questions that we used to motivate design-based inference, but adapt these to consider model-based inference.

2.3 Question 1: Population

The main advantage and disadvantage of relying on models is that they are abstract and theoretical, which means the connection between a model and the population it helps explain is less direct than with the design-based framework. Nevertheless, we need to clearly articulate our population of study – that is, who or what we want to learn about – since it is crucial for evaluating the types of modeling assumptions that will be sustainable.

As in the design-based setting, there is often a clear and distinct population such as “all registered voters” or “all Boston residents.” In other cases, the population may be more abstract. For example, a large multi-field literature has studied how the size of minority populations affects the views of the local majority population. Researchers in this space may be interested in making claims beyond the particular geographic region or minority/majority group, instead implicitly or explicitly considering a “superpopulation” of such cases that their model might explain. While there is nothing theoretically wrong with this approach, these ideas are often neglected in practice and the “scope conditions” of a particular model go unarticulated. The best quantitative work will be clear about what units or processes it is trying to learn about so that readers can evaluate how well the modeling assumptions fit that task.

2.4 Question 2: Statistical model

Let’s begin by building a bare-bones probability model for how our data came to be. As an example, suppose we have a data set with a series of numbers representing the ages, political party affiliations, and policy opinions of 1000 survey respondents. But we know that row 58 of our data could have produced a different set of numbers if another respondent had been selected as row 58 or if the original respondent gave a different opinion about immigration because they happened to see an immigration news story just before responding. To reason about this type of uncertainty precisely, we write $X_i$ as the random variable representing the value that row $i$ of some variable will take, before we see the data. The distribution of this random variable would tell us what types of data we should expect to see.

Why represent the data with random variables when we already know the value of the data itself? Why pretend we haven’t seen the data? The study of estimation from a frequentist perspective (which is the perspective of this book) focuses on the properties of estimators across repeated samples. In the example of the policy survey, this is akin to drawing a 1000 person sample repeatedly, each time including possibly different respondents in the sample. The random variable $X_i$ represents our uncertainty about what value, say, age will take for respondent $i$ in any of these samples, and the set $\{X_{1}, \ldots, X_{n}\}$ represents our uncertainty about the entire column of ages for all $n$ respondents. At the most general, the model-based approach says that these $n$ random variables follow some joint distribution, $F_{X_{1},\ldots,X_{n}}$, \[ \{X_{1}, \ldots, X_{n}\} \sim F_{X_{1},\ldots,X_{n}} \] The joint distribution $F$ here represents the probability model for the data. We have made no assumptions about it so far, so it could be any joint probability distribution over $n$ random variables. Note that this level of generality is difficult to work with in practice because there is essentially one draw from this joint distribution (the $n$ measurements in the data). The core question of modeling is about what restrictions a researcher puts on this joint distribution to make learning about it more tractable.

We focus on a relatively simple setting where we assume the data $\{X_1, \ldots, X_n\}$ are independent and identically distributed (iid) draws from a distribution with cumulative distribution function (cdf) $F$. They are independent in that information about any subset of random variable is not informative about any other subset of random variables, or, more formally, \[ F_{X_{1},\ldots,X_{n}}(x_{1}, \ldots, x_{n}) = F_{X_{1}}(x_{1})\cdots F_{X_{n}}(x_{n}) = \prod_{i=1}^n F(x_i) \] where $F_{X_{1},\ldots,X_{n}}(x_{1}, \ldots, x_{n})$ is the joint cdf of the random variable and $F_{X_{j}}(x_{j})$ is the marginal cdf of the $j$th random variable. They are “identically distributed” in the sense that each of the random variables $X_i$ have the same marginal distribution, $F$.

Note that we are being purposely vague about this cdf—it simply represents the unknown distribution of the data, otherwise known as the data generating process (DGP). Sometimes $F$ is also referred to as the population distribution or even just population, which has its roots in viewing the data as a random sample from some larger population.[^model] As a shorthand, we often say that the collection of random variables $\{X_1, \ldots, X_n\}$ is a random sample from population $F$ if $\{X_1, \ldots, X_n\}$ is iid with distribution $F$. The sample size $n$ is the number of units in the sample.

Note

You might wonder why we reference the distribution of $X_i$ with the cdf, $F$. Mathematical statistics tends to do this to avoid having to deal with discrete and continuous random variables separately. Every random variable – whether discrete or continuous – has a cdf, and the cdf contains all information about the distribution of a random variable.

Two metaphors help build intuition behind viewing the data as an iid draw from $F$:

Random sampling. Suppose we have a population of size $N$ that is much larger than our sample size $n$, and we take a random sample of size $n$ from this population with replacement. The distribution of the data in the random sample will be iid draws from the population distribution of the variables we are sampling. For example, suppose the population proportion of Democratic party identifiers among U.S. citizens is 0.33. If we randomly sample $n = 100$ U.S. citizens, each data point $X_i$ will be distributed Bernoulli with a probability of success (i.e., Democratic Party identifier) of 0.33.

Note that the last chapter explored simple random samples without replacement, which is a more common type of sampling – since generally people are selected into a survey once and they do not go back into the pool of potential survey takers. Sampling without replacement creates dependence across units, which would violate the iid assumption. However, if the population size $N$ is very large relative to the sample size $n$, this dependence will be very small, and the iid assumption will be relatively innocuous.

Groundhog Day. Random sampling does not always make sense as a justification for iid data, especially when the units are not samples at all but rather countries, states, or subnational units. (In these cases, the population can be the same as the sample – for example, using all 50 states to draw conclusions on the efficacy of state policy.) In this case, we have to appeal to a thought experiment where $F$ represents the fundamental uncertainty in the data-generating process. The metaphor here is that if we could re-run history many times, such as what happens to the protagonist played by Bill Murray in the 1993 American comedy movie Groundhog Day when he is magically forced to relive February 2 over and over again. Under this fiction, data and outcomes would change slightly due to the inherently stochastic nature of the world. In the movie, for example, Murray’s character starts off the same day in exactly the same way, but he begins to change his actions and the outcomes at the end of each day change in subtle ways. The iid assumption, then, is that each of the units in our data has the same DGP producing this data or the same distribution of outcomes under the Groundhog Day scenario. The set of all these infinite possible draws from the DGP is sometimes referred to as the superpopulation.

Note that there are other situations where the iid assumption is not appropriate, which we discuss in later chapters. But much of the innovation and growth in statistics over the last 50 years has been in figuring out how to make statistical inferences when iid does not hold. The solutions are often specific to the type of iid violation (e.g., spatial, time-series, network, clustered). As a rule of thumb, however, if the iid assumption may not be valid, any uncertainty statements will likely be overconfident. For example, confidence intervals, which we will cover in later chapters, are too small.

Finally, we introduced the data as a scalar random variable, but often our data has multiple variables. In that case, we easily modify $X_i$ to be a random vector (that is, a vector of random variables) and then $F$ becomes the joint distribution of that random vector. Nothing substantive changes about the above discussion.

Warning

Survey sampling is one of the most popular ways of obtaining samples from a population, but modern sampling practices rarely produce a “clean” set of $n$ iid responses. There are several reasons for this:

Modern random sampling techniques generally do not select every unit with the same probability. We might oversample certain groups for which we want more precise estimates, leading those groups to have a higher likelihood of being in the sample.
Response rates to surveys have been in steep decline and can often dip below 10%. Such non-random selection into the observed sample might lead to problems.
Internet polling is less costly than other forms of polling, but obtaining a list of population email addresses (or other digital contact information) to randomly sample is basically impossible. Large survey firms instead recruit large groups of panelists with known demographic information from which they can randomly sample in a way that matches population demographic information. Because the initial opt-in panel is not randomly sampled from the population, this procedure does not produce a true “random sample,” but, under certain assumptions, we can treat it like it is.

As discussed in the last chapter, there are ways to handle all of these issues (mostly through the use of survey weights), but it is important to realize that using a modern survey “as if” it was a simple random sample might lead to poor performance and incorrect inferences.

2.5 Question 3: Quantities of interest

In model-based inference, our goal is to learn about the data-generating process. Each data point $X_i$ represents a draw from a distribution, captured by the cdf $F$, and we would like to know more about this distribution. We might be interested in estimating the cdf at a general level or only some feature of the distribution, like a mean or conditional expectation function. We call these numerical features the quantities of interest. (Similarly, in the design-based inference framework we discussed in the previous chapter, the quantity of interest was a numerical summary of the finite population.)

The following are examples of frequently used quantities of interest:

Example 2.2 (Population mean) We may be interested in where the typical member of a population falls on some questions. Suppose we wanted to know the proportion of US citizens who support increasing legal immigration For citizen $i$, denote support as $Y_i = 1$. Our quantity of interest is then the mean of this random variable, $\mu = \E[Y_i] = \P(Y_{i} = 1)$. This is the same as the probability of randomly drawing someone from the population who supports increasing legal immigration.

Example 2.3 (Population variance) We may also be interested in variation in the population. For example, feeling thermometer scores are a common way to assess how survey respondents feel about a particular person or group. These ask each respondent to say how warmly he or she feels toward a group on a scale from 0 (cool) to 100 (warm), which we will denote $Y_i$. We might be interested in how polarized views are toward a group in the population, and one measure of polarization could be the variance, or spread, of the distribution of $Y_i$ around the mean. In this case, $\sigma^2 = \V[Y_i] = \E[(Y_i - \E[Y_i])^2]$ would be our quantity of interest.

Example 2.4 (RCT continued) Example 2.1 discussed a typical estimator for an experimental study with a binary treatment. The goal of that experiment is to learn about the difference between two conditional probabilities (or expectations): 1) the average support for increasing legal immigration in the treatment group, $\mu_1 = \E[Y_i \mid D_i = 1]$, and 2) the same average in the control group, $\mu_0 = \E[Y_i \mid D_i = 0]$. This difference, $\mu_1 - \mu_0$, is a function of unknown features of these two conditional distributions.

Each of these is a function of the (possibly joint) distribution of the data, $F$. In each of these, we are not necessarily interested in the entire distribution, just summaries of it (central tendency, spread). Of course, there are situations where we are also interested in the complete distribution. To speak about estimation in general, we will let $\theta$ represent some generic quantity of interest. Point estimation describes how we obtain a single “best guess” about $\theta$.

Note

Some refer to quantities of interest as parameters or estimands (that is, the target of estimation).

2.6 Question 4: Estimator

Having a target in mind, we can estimate it with our data. To do so, we first need a rule or algorithm or function that takes as inputs the data and returns a best guess about the quantity of interest. One of the most popular and useful algorithm would be to sum all the data points and divide by the number of points: \[ \frac{X_1 + X_2 + \cdots + X_n}{n}. \] This, the much-celebrated sample mean, provides a rule for how produce a single-number summary of the data. To go one pedantic step further and define it as a function of the data more explicitly: \[ \textsf{mean}(X_1, X_2, \ldots, X_n) = \frac{X_1 + X_2 + \cdots + X_n}{n}. \] We can use this model to provide a definition for an arbitrary estimator for an arbitrary quantity of interest.

Definition 2.1 An estimator $\widehat{\theta}_n = \theta(X_1, \ldots, X_n)$ for some parameter $\theta$, is a function of the data intended as a guess about $\theta$.

Note

It is widespread, though not universal, to use the “hat” notation to define an estimator and its estimand. For example, $\widehat{\theta}$ (or “theta hat”) indicates that this estimator is targeting the parameter $\theta$.

Example 2.5 (Estimators for the population mean) Suppose our goal is to estimate the population mean of $F$, which we will represent as $\mu = \E[X_i]$. We could choose from several estimators, all with different properties. \[ \widehat{\theta}_{n,1} = \frac{1}{n} \sum_{i=1}^n X_i, \quad \widehat{\theta}_{n,2} = X_1, \quad \widehat{\theta}_{n,3} = \text{max}(X_1,\ldots,X_n), \quad \widehat{\theta}_{n,4} = 3 \] The first is just the sample mean, which is an intuitive and natural estimator for the population mean. The second just uses the first observation. While this seems silly, this is a valid statistic since it is a function of the data! The third takes the maximum value in the sample, and the fourth always returns three, regardless of the data. These are also valid statistics.

When we view the data $\{X_{1}, \ldots, X_{n}\}$ as a collection of random variables, then any function of them is also a random variable. Thus, we can view $\widehat{\theta}_n$ as a random variable that has a distribution induced by the randomness of the sample. Drawing two different samples of respondents will lead to two different estimates. For example, here we illustrate two samples of size $n =5$ from the population distribution of a binary variable:

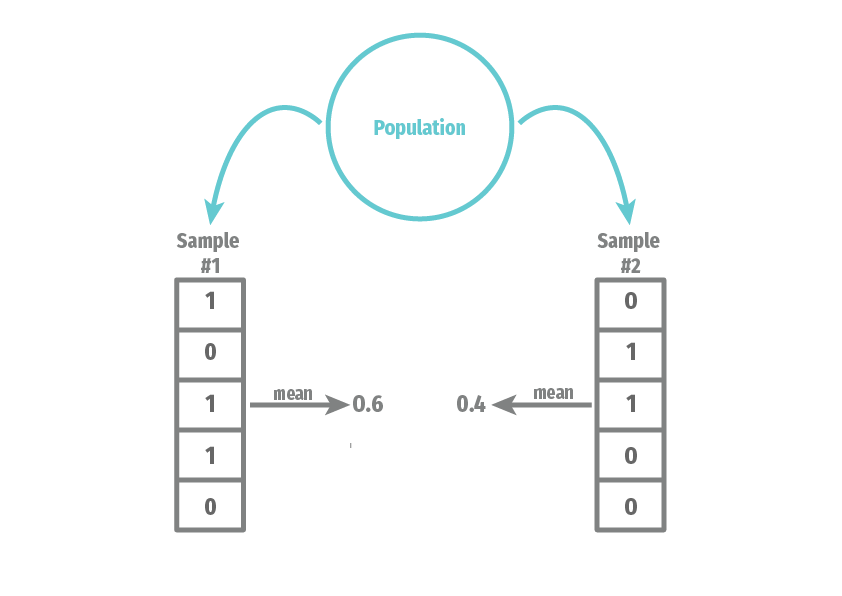
We can see that the mean of the variable depends on what exact values end up in our sample. We refer to the distribution of $\widehat{\theta}_n$ across repeated samples as its sampling distribution. The sampling distribution of an estimator will be the basis for all of the formal statistical properties of an estimator.

Warning

One important distinction of jargon is between an estimator and an estimate. The estimator is a function of the data, whereas the estimate is the realized value of the estimator once we see the data (that is, the data are realized). The estimator is a random variable that has uncertainty over what value it will take, and we represent the estimator as a function of random variables, $\widehat{\theta}_n = \theta(X_1, \ldots, X_n)$. An estimate is a single number, such as 0.38, that we calculated in R with our data (our draw from $F$). Formally, the estimate is $\theta(x_1, \ldots, x_n)$ when the data is $\{X_1, \ldots, X_n\} = \{x_1, \ldots, x_n\}$, whereas we represent the estimator as a function of random variables, $\widehat{\theta}_n = \theta(X_1, \ldots, X_n)$.

2.7 How to find estimators

Where do estimators come from? That may seem like a question reserved for statisticians or methodologists or others responsible for “developing new methods.” But knowing how estimators are derived is valuable even if we never plan to do it ourselves. Knowing where an estimator comes from provides strong insights into its strengths and weaknesses. We will briefly introduce estimators based on parametric models, before turning to the main focus of this book, plug-in estimators.

2.7.1 Parametric models and maximum likelihood

The first method for generating estimators relies on parametric models, in which the researcher specifies the exact distribution (up to some unknown parameters) of the DGP. Let $\theta$ be the parameters of this distribution, where $\{X_1, \ldots, X_n\}$ be iid draws from $F_{\theta}$. We should also formally state the set of possible values the parameters can take, which we call the parameter space, denoted by $\Theta$. Because we assume we know the distribution of the data, we can write the probability density function, or pdf, as $f(X_i \mid \theta)$ and define the likelihood function as the product of these pdfs over the units as a function of the parameters: \[ L(\theta) = \prod_{i=1}^n f(X_i \mid \theta). \] We can then define the maximum likelihood estimator (MLE) for $\theta$ as the values of the parameter that, well, maximize the likelihood: \[ \widehat{\theta}_{mle} = \argmax_{\theta \in \Theta} \; L(\theta) \] Sometimes we can use calculus to derive a closed-form expression for the MLE. At other times we use iterative techniques that search the parameter space for the maximum.

Maximum likelihood estimators have nice properties, especially in large samples. Unfortunately, they also require the correct knowledge of the parametric model, which is often difficult to justify. Do we really know if we should model a given event count variable as Poisson or Negative Binomial? The attractive properties of MLE are only as good as the ability to specify the parametric model.

No free lunch

Building up intuition about the assumptions-precision tradeoff is essential. Researchers can usually get more precise estimates if they make stronger and potentially more fragile assumptions. Conversely, they will almost always get less accurate estimates when weakening the assumptions.

2.7.2 Plug-in estimators

The second broad class of estimators is semiparametric in that we specify some finite-dimensional parameters of the DGP but leave the rest of the distribution unspecified. For example, we might define a population mean, $\mu = \E[X_i]$ and a population variance, $\sigma^2 = \V[X_i]$ but leave the shape of the distribution unrestricted. This ensures that our estimators will be less dependent on correctly specifying distributions about which we have little intuition or knowledge.

The primary method for constructing estimators in this setting is to use the plug-in estimator, or the estimator that replaces any population mean with a sample mean. Obviously, in the case of estimating the population mean, $\mu$, we will use the sample mean as the estimate: \[ \Xbar_n = \frac{1}{n} \sum_{i=1}^n X_i \quad \text{estimates} \quad \E[X_i] = \int_{\mathcal{X}} x f(x)dx \] In plain language, we are replacing the unknown population distribution $f(x)$ in the population mean with a discrete uniform distribution over our data points, with $1/n$ probability assigned to each unit. Why do this? It encodes that, if we have a random sample, our best guess about the population distribution of $X_i$ is the sample distribution in our observed data. If this intuition fails, you can hold onto an analog principle: sample means of random variables are natural estimators of population means.

What about estimating something more complicated, like the expected value of a function of the data, $\theta = \E[r(X_i)]$? The key is to see that $r(X_i)$ is also a random variable. Let this random variable be $Y_i = r(X_i)$. Now we can see that $\theta$ is just the population expectation of this random variable. Using the plug-in estimator gives us: \[ \widehat{\theta} = \frac{1}{n} \sum_{i=1}^n Y_i = \frac{1}{n} \sum_{i=1}^n r(X_i). \]

These facts enable us to describe a more general plug-in estimator. To estimate some quantity of interest that is a function of population means, we can generate a plug-in estimator by replacing any population mean with a sample mean. Formally, let $\alpha = g\left(\E[r(X_i)]\right)$ be a parameter that is defined as a function of the population mean of a (possibly vector-valued) function of the data. We can then estimate this parameter by plugging in the sample mean for the population mean to get the plug-in estimator, \[ \widehat{\alpha} = g\left( \frac{1}{n} \sum_{i=1}^n r(X_i) \right) \quad \text{estimates} \quad \alpha = g\left(\E[r(X_i)]\right) \] This approach to plug-in estimation with sample means is very general and will allow us to derive estimators in various settings.

Example 2.6 (Estimating population variance) The population variance of a random variable is $\sigma^2 = \E[(X_i - \E[X_i])^2]$. To derive a plug-in estimator for this quantity, we replace the inner $\E[X_i]$ with $\Xbar_n$ and the outer expectation with another sample mean: \[ \widehat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^n (X_i - \Xbar_n)^2. \] This plug-in estimator differs from the standard sample variance, which divides by $n - 1$ rather than $n$. This minor difference does not matter in moderate to large samples.

Example 2.7 (Estimating population covariance) Suppose we have two variables, $(X_i, Y_i)$. A natural quantity of interest here is the population covariance between these variables, \[ \sigma_{xy} = \text{Cov}[X_i,Y_i] = \E[(X_i - \E[X_i])(Y_i-\E[Y_i])], \] which has the plug-in estimator, \[ \widehat{\sigma}_{xy} = \frac{1}{n} \sum_{i=1}^n (X_i - \Xbar_n)(Y_i - \Ybar_n). \]

Notation alert

Given the connection between the population mean and the sample mean, you may see the $\E_n[\cdot]$ operator used as a shorthand for the sample average: \[ \E_n[r(X_i)] \equiv \frac{1}{n} \sum_{i=1}^n r(X_i). \]

Finally, plug-in estimation goes beyond just replacing population means with sample means. We can derive estimators of the population quantiles like the median with sample versions of those quantities. These approaches are unified in replacing the unknown population cdf, $F$, with the empirical cdf, \[ \widehat{F}_n(x) = \frac{\sum_{i=1}^n \mathbb{I}(X_i \leq x)}{n}, \] where $\mathbb{I}(A)$ is an indicator function that takes the value 1 if the event $A$ occurs and 0 otherwise. For a more complete and technical treatment of these ideas, see Wasserman (2004) Chapter 7.

2.8 The three distributions: population, empirical, and sampling

Once we start to wade into estimation, there are several distributions to keep track of, and things can quickly become confusing. Three specific distributions are all related and easy to confuse, but keeping them distinct is crucial.

The population distribution is the distribution of the random variable, $X_i$, which we have labeled $F$ and is our target of inference. The empirical distribution is the distribution of the actual realizations of the random variables in our samples, $X_1, \ldots, X_n$ (that is, the values that we eventually observe in our data frame). Because this is a random sample from the population distribution and can serve as an estimator of $F$, we sometimes call this $\widehat{F}_n$.

Separately from both is the sampling distribution of an estimator, which is the probability distribution of $\widehat{\theta}_n$. This represents the uncertainty around our estimate before we see the data. Remember that our estimator is itself a random variable because it is a function of random variables: the data itself. That is, we defined the estimator as $\widehat{\theta}_n = \theta(X_1, \ldots, X_n)$.

Example 2.8 (Likert responses) Suppose $X_i$ is the answer to the question “How much do you agree with the following statement: Immigrants are a net positive for the United States,” where $X_i = 0$ is “strongly disagree,” $X_i = 1$ is “disagree,” $X_i = 2$ is “neither agree nor disagree,” $X_i = 3$ is “agree,” and $X_i = 4$ is “strongly agree.”

The population distribution describes the probability of randomly selecting a person with each one of these values, $\P(X_i = x)$. The empirical distribution would be the fraction of our observed data taking each value. And the sampling distribution of the sample mean, $\Xbar_n$, would be the distribution of the sample mean recalculated across repeated samples from the population.

Suppose the population distribution of $X_i$ followed a binomial distribution with five trials and probability of success in each trial of $p = 0.4$. We could generate one sample with $n = 10$ and thus one empirical distribution using rbinom():

my_samp <- rbinom(n = 10, size = 4, prob = 0.4)
my_samp

 [1] 1 2 1 3 3 0 2 3 2 1

table(my_samp)

my_samp
0 1 2 3 
1 3 3 3

We obtain one draw from the sampling distribution of $\Xbar_n$ by taking the mean of this sample:

mean(my_samp)

[1] 1.8

If we had a different sample,however, we would obtain a different empirical distribution and thus get a different estimate of the sample mean:

my_samp2 <- rbinom(n = 10, size = 4, prob = 0.4)
mean(my_samp2)

[1] 1.6

The sampling distribution is the distribution of these sample means across repeated sampling.

2.9 Finite-sample properties of estimators

As discussed in our introduction to estimators, their usefulness depends on how well they help us learn about the quantity of interest. If we get an estimate $\widehat{\theta} = 1.6$, we would like to know that this is “close” to the true parameter $\theta$. The sampling distribution is key to answering these questions. Intuitively, we would like the sampling distribution of $\widehat{\theta}_n$ to be as tightly clustered around the true $\theta$ as possible. Here, though, we run into a problem: the sampling distribution depends on the population distribution since it is about repeated samples of the data from that distribution filtered through the function $\theta()$. Since $F$ is unknown, this implies that the sampling distribution will also usually be unknown.

Even though we cannot precisely pin down the entire sampling distribution, we can use assumptions to derive specific properties of the sampling distribution that are useful in comparing estimators. Note that the properties here will be very similar to the

2.9.1 Bias

The first property of the sampling distribution concerns its central tendency. In particular, we define the bias (or estimation bias) of estimator $\widehat{\theta}$ for parameter $\theta$ as \[ \text{bias}[\widehat{\theta}] = \E[\widehat{\theta}] - \theta, \] which is the difference between the mean of the estimator (across repeated samples) and the true parameter. All else equal, we would like the estimation bias to be as small as possible. The smallest possible bias, obviously, is 0, and we define an unbiased estimator as one with $\text{bias}[\widehat{\theta}] = 0$ or equivalently, $\E[\widehat{\theta}] = \theta$.

However, all else is not always equal, and unbiasedness is not a property to which we should become overly attached. Many biased estimators have other attractive properties, and many popular modern estimators are biased.

Example 2.9 (Unbiasedness of the sample mean) The sample mean is unbiased for the population mean when the data is iid and $\E|X| < \infty$. In particular, we apply the rules of expectations: \[\begin{aligned} \E\left[ \Xbar_n \right] &= \E\left[\frac{1}{n} \sum_{i=1}^n X_i\right] & (\text{definition of } \Xbar_n) \\ &= \frac{1}{n} \sum_{i=1}^n \E[X_i] & (\text{linearity of } \E)\\ &= \frac{1}{n} \sum_{i=1}^n \mu & (X_i \text{ identically distributed})\\ &= \mu. \end{aligned}\] Notice that we only used the “identically distributed” part of iid. Independence is not needed.

Warning

Properties like unbiasedness might only hold for a subset of DGPs. For example, we just showed that the sample mean is unbiased but only when the population mean is finite. There are probability distributions like the Cauchy that are not finite and where the expected value diverges. Thus, here we are dealing with a restricted class of DGPs that rules out such distributions. This is sometimes formalized by defining a class $\mathcal{F}$ of distributions; unbiasedness might hold in that class if it is unbiased for all $F \in \mathcal{F}$.

2.10 Question 5: Uncertainty

The spread of the sampling distribution is also important. We define the sampling variance as the variance of an estimator’s sampling distribution, $\V[\widehat{\theta}]$, which measures how spread out the estimator is around its mean. For an unbiased estimator, lower sampling variance implies the distribution of $\widehat{\theta}$ is more concentrated around the true value of the parameter.

Example 2.10 (Sampling variance of the sample mean) We can prove that the sampling variance of the sample mean of iid data for all $F$ such that $\V[X_i]$ is finite (more precisely, $\E[X_i^2] < \infty$)

\[\begin{aligned} \V\left[ \Xbar_n \right] &= \V\left[ \frac{1}{n} \sum_{i=1}^n X_i \right] & (\text{definition of } \Xbar_n) \\ &= \frac{1}{n^2} \V\left[ \sum_{i=1}^n X_i \right] & (\text{property of } \V) \\ &= \frac{1}{n^2} \sum_{i=1}^n \V[X_i] & (\text{independence}) \\ &= \frac{1}{n^2} \sum_{i=1}^n \sigma^2 & (X_i \text{ identically distributed}) \\ &= \frac{\sigma^2}{n} \end{aligned}\]

As we discussed before, an alternative measure of spread for any distribution is the standard deviation, which is on the same scale as the original random variable. The standard deviation of the sampling distribution of $\widehat{\theta}$ is known as the standard error of $\widehat{\theta}$: $\se(\widehat{\theta}) = \sqrt{\V[\widehat{\theta}]}$.

Given the above derivation, the standard error of the sample mean under iid sampling is $\sigma / \sqrt{n}$.

2.10.1 Mean squared error

Bias and sampling variance measure two properties of “good” estimators because they capture the fact that we want the estimator to be as close as possible to the true value. One summary measure of the quality of an estimator is the mean squared error or MSE, which is
\[ \text{MSE} = \E[(\widehat{\theta}_n-\theta)^2]. \] We would ideally have this be as small as possible!

The MSE also relates to the bias and the sampling variance (provided it is finite) via the following decomposition result: \[ \text{MSE} = \text{bias}[\widehat{\theta}_n]^2 + \V[\widehat{\theta}_n] \tag{2.1}\] This decomposition implies that, for unbiased estimators, MSE is the sampling variance. It also highlights why we might accept some bias for significant reductions in variance for lower overall MSE.

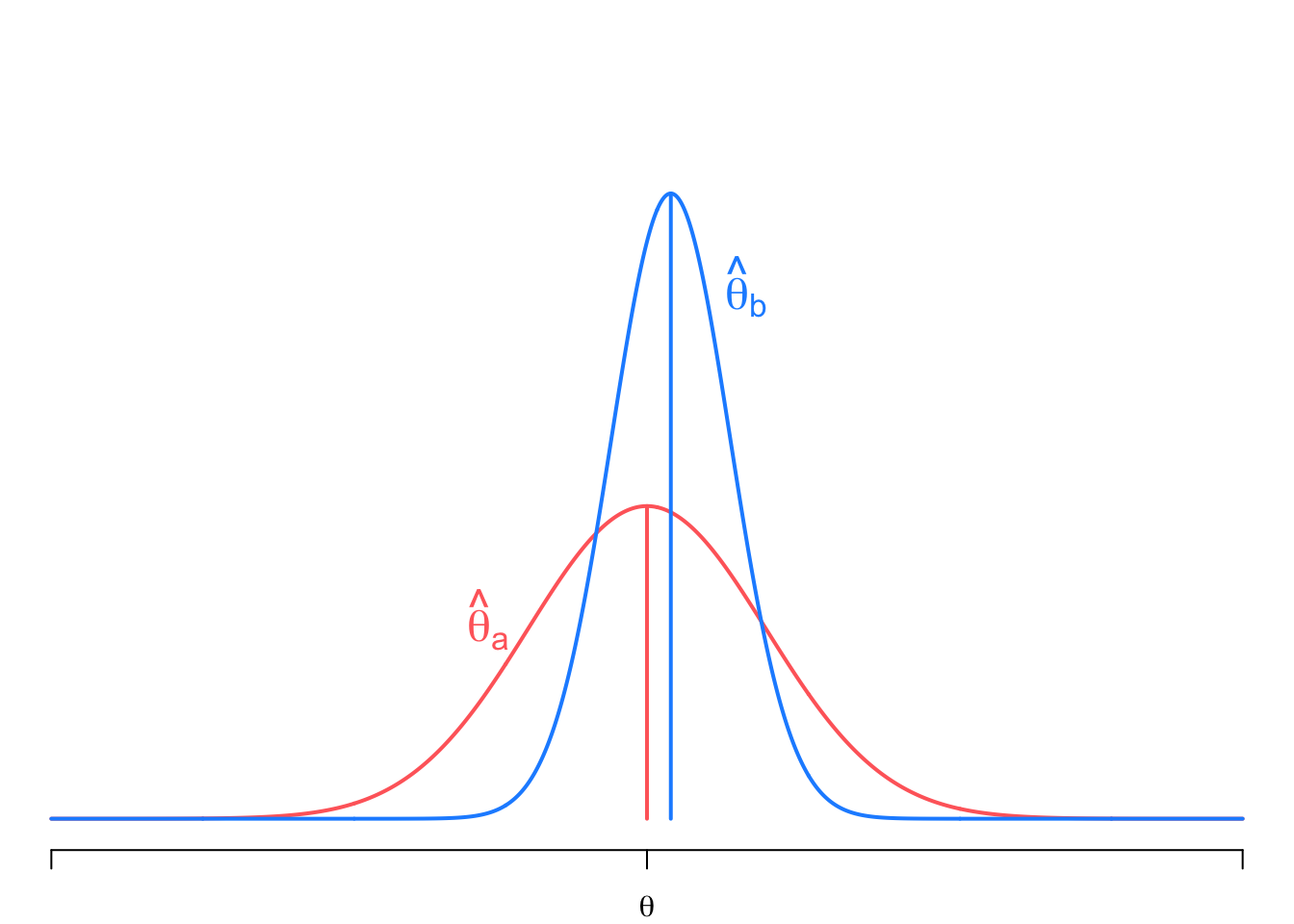
This figure shows the sampling distributions of two estimators: (1) $\widehat{\theta}_a$, which is unbiased (centered on the true value $\theta$) but with a high sampling variance, and (2) $\widehat{\theta}_b$, which is slightly biased but with much lower sampling variance. Even though $\widehat{\theta}_b$ is biased, the probability of drawing a value close to the truth is higher than for $\widehat{\theta}_a$. The MSE helps capture this balancing between bias and variance, and, indeed, in this case, $MSE[\widehat{\theta}_b] < MSE[\widehat{\theta}_a]$.

2.11 Summary

In this chapter, we introduced model-based inference, in which we posit a probability model for the data-generating process. These models can be parametric in the sense that we specify the probability distribution of the data up to some parameters. They can also be semiparametric where we only specify certain features of the distribution such as a finite mean and variance. This chapter mostly focused on the latter, where we assumed the observed data were independent and identically distributed draws from a population distribution with finite mean and variance.

An estimator is a function of the data meant as a guess for some quantity of interest in the population. Because it is a function of random variables (the data), estimators are also random variables and have distributions, called sampling distributions, across repeated draws from the population. If this distribution is centered on the true value of the quantity of interest, we call the estimator unbiased. The variance of the sampling distribution, called the sampling variance, tells us how variable we should expect the estimator to be across draws from the population. The mean-squared error is an overall measure of the accuracy of an estimator that combines notions of bias and sampling variance.

We showed in this chapter that the sample mean is unbiased for the population mean and that the sampling variance of the sample mean is the ratio of the population variance to the sample size. We also saw that plug-in estimators are a powerful way of constructing estimators as functions of sample means. That said, the focus of this chapter was finite-sample properties (that is, properties that are true no matter the sample size). In the next chapter, we will derive even more powerful results using large-sample approximations.

1924 May 24, Boston Herald, Whiting’s Column: Tammany Has Learned That This Is No Time for Political Bosses, Quote Page 2, Column 1, Boston, Massachusetts. (GenealogyBank)↩︎