Game changers: Detecting shifts in overdispersed count data
Political Analysis, Vol. 26, No. 2 (2018): 230-239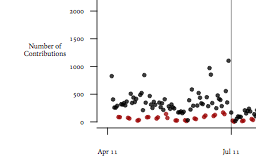
In this paper, I introduce a Bayesian model for detecting changepoints in a time series of overdispersed count data, such as contributions to candidates over the course of a campaign or counts of terrorist violence. While many extant changepoint models force researchers to choose the number of changepoint ex ante, this model incorporates a hierarchical Dirichlet process prior in order to estimate the number of changepoints as well as their location. This allows researchers to discover salient structural breaks and perform inference on the number of such breaks in a given time series. I demonstrate the usefulness of the model with applications to campaign contributions in the 2012 U.S. Republican presidential primary and incidences of global terrorism from 1970 to 2015.